- Moi, j'ai dit "bizarre bizarre", comme c'est étrange ! Pourquoi aurais je dit "bizarre bizarre" ?
- Je vous assure mon cher cousin, que vous avez dit "bizarre bizarre".
- Moi, j'ai dit bizarre, comme c'est bizarre !
Drôle de Drame

Tous cousins? Comme c'est bizarre!

Chacun a fait un jour ce calcul simple: deux parents, quatre grands-parents, huit arrière-grands-parents et ainsi de suite. On sait que cela aboutit vite à une absurdité. Au bout de trente générations (environ mille ans), le nombre théorique d'ascendants ainsi calculé dépasse le milliard, soit bien plus que la population mondiale de l'époque. L'explication est simple. Nous descendons de chacun de nos ancêtres par différentes lignées, un phénomène appelé savamment implexe fort bien décrit dans Wikipédia. Et si on remonte "assez loin" dans le temps, nous avons tous les mêmes ancêtres. Ce "assez loin" est toutefois difficile à établir, les études et modèles divers le situant entre 1000 et 5000 ans dans le passé.

Mais tout cela ne répond pas à la question pratique. Combien faut-il de générations pour que deux individus pris au hasard dans une population (européenne par exemple) de 2018 aient une bonne probabilité (supérieure à 90% par exemple) de se trouver un ancêtre commun? Et, question subsidiaire, peuvent-ils espérer le trouver par les moyens classiques de la généalogie, c'est-à-dire les archives?

On va tenter ici une approche qui peut donner des ordres de grandeur, sans bien sûr prétendre répondre précisément à cette question. Il s'agit de calculer la probabilité pour que deux échantillons d'ancêtres (de taille égale à k) dans une population donnée dans le passé (de taille égale à N) aient au moins un élément commun. Si on assimile le choix de ces échantillons à un tirage "avec remise" (deux ancêtres pouvant être identiques), on obtient la formule assez simple ci-dessous. On calcule en fait la probabilité pour que les échantillons soient disjoints (aucun individu commun) et on soustrait cette valeur à 1 pour l'événement complémentaire (au moins un élément commun). Le lecteur un peu frotté de calcul de probabilités pourra vérifier à titre d'exercice la validité de cette formule.

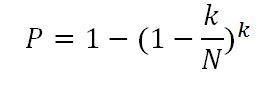
Si on applique cette formule pour différentes tailles de population et d'échantillons, on obtient le tableau suivant:

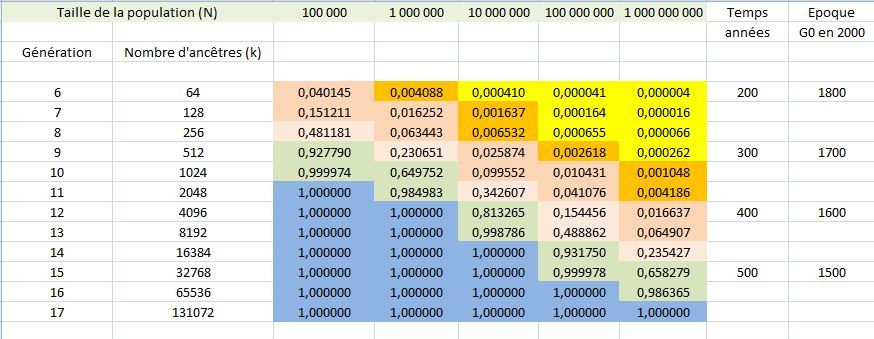
Comme dans le fameux paradoxe des anniversaires, un problème assez similaire d'ailleurs, les résultats peuvent sembler contre-intuitifs. Prenons un exemple: pour k=2048 et N= 1000000, la probabilité que les deux échantillons aient au moins un élément commun est de plus de 98%, alors que les échantillons ne représentent qu'un peu plus de 0,2% de la population totale! Si le modèle correspondait un tant soit peu à la réalité, cela signifierait que deux individus quelconques dans une même population d'un million d'habitants auraient plus de 98% de chance d'avoir au moins un ancêtre commun à la 11ème génération, c'est-à-dire dans la première moitié du 17ème siècle s'ils sont nés au début du 21ème siècle. Si on multiplie la population de référence par 100, à la même époque la probabilité n'est que de 4%, mais il suffit de remonter quatre générations pour qu'elle dépasse 99,99% vers l'an 1500. Cent millions, c'est le double de la population européenne en 1400 (la Grande Peste et la guerre de Cent Ans sont passées par là).

Bien sûr, ce modèle est basé sur des hypothèses ultra-simplificatrices, mais il est intéressant de noter d'une part la rapidité avec laquelle la probabilité d'ancêtres communs bascule du très improbable (moins de 1%) au très probable (plus de 99%) en quelques générations, moins de deux siècles quelle que soit la taille de la population de référence, et d'autre part que multiplier la taille de la population de référence par 100 ne fait que reporter le phénomène un siècle plus tôt.

Ironie de l'affaire, le basculement de l'improbable au quasi-certain se fait (pour une population de référence de 10 à 100 millions), dans le courant du 16ème siècle pour des enfants nés au début du 21ème. Or, pour le commun des mortels généalogistes, le 16ème siècle c'est justement cet horizon quasi-impossible à franchir si les seules sources sont les registres d'état-civil ou des paroisses. Mais ceux qui ont la chance de trouver au moins une lignée d'ancêtres qui traverse le tunnel du 15ème siècle constatent en général qu'elle va se raccrocher sans trop de difficulté à un buisson historique de "grandes familles", et se découvrent descendants de Hugues Capet, Guillaume le Conquérant etc, et donc cousins de toutes les familles royales d'Europe. Et quand deux de ceux-là se cherchent un cousinage, ils arrivent la plupart du temps à le trouver quelque part entre 1300 et 1500. Voyez la dernière recrue de la famille royale d'Angleterre. Les généalogistes ont bien vite déniché une parenté entre la belle Meghan et son Harry de prince. Et à quelle époque? L'ancêtre commune des deux tourtereaux, du moins la plus récente identifiée, est une certaine Mary Clifford. Ses dates? 1416-1478. No comment.

Est-ce à dire que tous les autres, comme mes paysans d'ancêtres dont le nom n'est écrit nulle part avant l'ordonnance de Villers-Cotterêts, ne se raccrocheraient pas à ce même tronc commun? Les chiffres précédents semblent indiquer le contraire, sauf à croire à une stricte endogamie de l'aristocratie pendant des siècles, à nier l'évidence des enfants "illégitimes" et donc bien sûr non documentés, des fils et filles déchu(e)s de leurs droits, déshérités, les aventuriers partis chercher fortune hors de leurs terres et milieux d'origine, et toutes celles et ceux que calamités naturelles, guerres et pillages ont jetés à toute époque sur les chemins de l'exil. Et il faut bien garder en tête qu'un seul "étranger" dans la famille amène derrière lui tous ses ancêtres, et en cherchant bien, ou même sans trop chercher, on finit par trouver dans son arbre un bon vieux bâtard, comme mon ancêtre Guillaume Jégou, sieur de Roch an Bosc.

Une note optimiste pour finir. Pour nos descendants nés vers 2100, le siècle critique ne sera plus le 16ème mais le 17ème, beaucoup mieux documenté. Et vers 2200, ce sera un jeu d'enfant que d'établir son cousinage avec n'importe qui, les ancêtres communs se situant avec une forte probabilité au début du 18ème. D'autant plus que notre époque voit un brassage de population sans précédent sans doute (en Europe du moins) depuis la chute de l'Empire Romain et les grandes invasions, qui rendra sans doute le modèle présenté ci-dessus de plus en plus proche de la réalité.